Nos preguntábamos la semana pasada por qué son solo 92 las soluciones del problema de las 8 reinas, dado que hay 12 esencialmente distintas y cada una de ellas puede dar lugar a 8 mediante rotaciones y reflexiones, por lo que deberían ser 12 x 8 = 96. La explicación es que una de las 12 soluciones básicas tiene simetría central, por lo que no varía al girarla 180º, y, análogamente, al girarla 270º obtenemos la misma configuración que al girarla 90º; por tanto, esta solución simétrica (¿puedes hallarla?) solo da lugar a 2 distintas por rotación y otras 2 por reflexión: 4 en vez de 8, y el total será, pues, 11 x 8 + 4 = 92.
En cuanto al problema de los caballos de Guarini, es evidente que cada caballo necesita un mínimo de 2 movimientos para llegar a otra esquina del tablero de 3x3, por lo que la solución requerirá un mínimo de 8 movimientos. En realidad, hacen falta el doble, es decir, 16. Para ver con más claridad los recorridos necesarios, conviene convertir el tablero en un grafo octogonal, en el que cada nodo (vértice) representa una casilla y cada arista un posible movimiento de caballo de una casilla a otra; en la posición inicial, los caballos ocupan nodos alternos. Pero, ¿por qué 8 nodos si las casillas del tablero de 3x3 son 9? Pues porque la casilla central no es alcanzable en ningún momento para ningún caballo, y a efectos de los recorridos posibles es como si no existiera.
El último problema de la semana pasada consistía en hallar un recorrido completo de caballo en un tablero de 3x4 partiendo de una esquina. He aquí una solución:
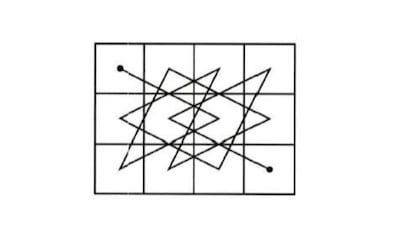
¿Cuántas soluciones distintas hay? ¿Y si el caballo parte de otra casilla?
Grafos, trenes y relaciones
Y hablando de los grafos y de su utilidad para abordar todo tipo de situaciones en las que una serie de elementos se conectan o relacionan de diversas maneras, veamos algunos problemas que, al igual que los anteriores, se simplifican al dotarlos de una adecuada —nunca mejor dicho— representación “gráfica”:
1. Demostrar que en cualquier grupo de dos o más personas hay al menos dos de ellas que tienen el mismo número de amigos dentro del grupo.
2. Una forma de conectar por una futura red de vías de altísima velocidad las 15 comunidades autónomas peninsulares sería la centralista (es decir, la actual): desde Madrid se trazan sendas vías rectilíneas a las capitales de las otras 14 comunidades. Pero si, al caer en la cuenta de que no es imprescindible pasar por Madrid para ir, por ejemplo, de Oviedo a Bilbao, quisiéramos minimizar la longitud total de vías construidas, ¿cómo tendríamos que abordar el problema?
Y no se puede hablar de grafos sin mencionar a Clara Grima, así que nada mejor, para terminar, que un problema sacado de su estupendo libro En busca del grafo perdido:
3. Ana y Blas asisten a una fiesta junto con otras cuatro parejas. Al encontrarse, algunos se saludan con un apretón de manos y otros con un beso. Al acabar la fiesta, Blas pregunta a los asistentes a cuánta gente ha dado la mano al saludar y recibe nueve respuestas diferentes. ¿A cuántas personas ha dado la mano Ana?
Tu suscripción se está usando en otro dispositivo
¿Quieres añadir otro usuario a tu suscripción?
Si continúas leyendo en este dispositivo, no se podrá leer en el otro.
FlechaTu suscripción se está usando en otro dispositivo y solo puedes acceder a EL PAÍS desde un dispositivo a la vez.
Si quieres compartir tu cuenta, cambia tu suscripción a la modalidad Premium, así podrás añadir otro usuario. Cada uno accederá con su propia cuenta de email, lo que os permitirá personalizar vuestra experiencia en EL PAÍS.
¿Tienes una suscripción de empresa? Accede aquí para contratar más cuentas.
En el caso de no saber quién está usando tu cuenta, te recomendamos cambiar tu contraseña aquí.
Si decides continuar compartiendo tu cuenta, este mensaje se mostrará en tu dispositivo y en el de la otra persona que está usando tu cuenta de forma indefinida, afectando a tu experiencia de lectura. Puedes consultar aquí los términos y condiciones de la suscripción digital.
Sobre la firma