Bernard Morin, haciendo matemáticas a ciegas

Desde pequeños, la enseñanza y el aprendizaje de las matemáticas están íntimamente ligados a la vista. Aparte de las razones evidentes, una característica muy importante de la enseñanza de las matemáticas es mostrarlas visualmente, y una de las principales partes del aprendizaje en matemáticas es adquirir conocimientos desde la visualización de las mismas.

Por ello, creo que es razonable considerar que es complicadísimo aprender matemáticas sin el sentido de la vista. En realidad, las limitaciones que conlleva no contar con visión hacen que sea muy difícil avanzar en el aprendizaje de cualquier rama, pero quizás con las matemáticas sea más complicado aún.

Y no digamos ya “hacer” matemáticas de alto nivel. A muchos les habrá venido a la cabeza el caso del gran Leonhard Euler, el matemático más prolífico de la historia. Euler pasó los últimos 17 años de su vida ciego de ambos ojos (primero perdió el derecho y después el izquierdo). Pero eso no hizo que su productividad disminuyera, más bien todo lo contrario. Siguió produciendo trabajos matemáticos (muchos dictados a su hijo mayor), ayudado por su gran capacidad de cálculo y su memoria fotográfica…

…pero Euler ya sabía matemáticas (y muchas) antes de quedarse ciego. La cuestión es: ¿se puede llegar a máximo nivel en matemáticas siendo ciego desde pequeño?

Pues la respuesta es sí, aunque no sea fácil sí se puede llegar a ser un matemático de alto nivel aun sufriendo ceguera. Y, aunque no es el único, uno de los matemáticos ciegos más influyentes de la historia es el eje central de nuestro artículo de hoy: Bernard Morin.

Bernard Morin, matemático francés nacido en 1931, es especialista en Topología, rama de las matemáticas que, a grandes rasgos, estudia las propiedades de los objetos geométricos que no cambian mediante deformaciones continuas (por ejemplo, podemos estirar pero no podemos romper). En Topología, es de sobra conocida la frase siguiente:

Para un topólogo, no hay diferencia entre un dónut y una taza de café.

La razón es que podemos deformar de manera continua (sin romper o rasgar) una taza de café y convertirla en una figura en forma de dónut, y viceversa.

Volvamos a nuestro protagonista. Bernard Morin se quedó ciego a los 6 años a causa de un glaucoma, razón por la cual asistió a colegios especiales para ciegos hasta su adolescencia, ingresando después en un liceo. Los intereses académicos de Morin eran, principalmente, las matemáticas y la filosofía, pero su padre le dirigió hacia ésta última (pensaba que su hijo nunca podría destacar en matemáticas).

El caso es que, más adelante, Bernard dejó la filosofía y se centró en las matemáticas. Y destacó, no cabe duda. Tanto que ingresó en el CNRS, teniendo a Henri Cartan como mentor. También pasó dos años en el Instituto de Estudios Avanzados de Princeton a la vez que terminaba su tesis, bajo la dirección de René Thom. Después, dedicó gran parte de su carrera a enseñar en la Universidad de Estrasburgo, donde se retiró en 1999.

Dicho esto, vayamos al turrón. ¿Qué aportaciones ha hecho Morin a las matemáticas? Como decíamos antes, su campo principal de estudio fue la Topología, y ahí fue donde Bernard Morin realizó aportaciones más que interesantes. Posiblemente, la más relevante tiene que ver con algo tan simple como una esfera.

En 1959, Stephen Smale había demostrado un resultado del cual se deduce que se puede evertir una esfera. ¿Qué es eso de evertir una esfera? Pues algo así como darle la vuelta. Más concretamente, evertir una esfera es deformarla (sin romperla) de manera que la parte externa quede dentro y la parte interna quede fuera (permitimos que haya autointersecciones si es necesario). Podéis intentar pensar en alguna forma de hacer eso con una esfera, pero os adelanto que es algo muy muy muy, pero que muy, complicado.

Smale había demostrado que se podía hacer, pero no se sabía cómo. Y ahí es donde entra nuestro amigo. Bernard Morin fue uno de los matemáticos que desarrollo una manera de evertir una esfera. Utilizando ideas propias y otras que le comunicó Arnold Shapiro, y con la ayuda del físico Marcel Froissart, Morin consiguió hacer realidad lo que Smale solamente había demostrado que existía.

Queréis verlo, ¿verdad? Os entiendo, yo también querría. Pues aquí lo tenéis, en vídeo. Queridos lectores, os presento la eversión de la esfera:

No me digáis que no es impresionante. Y no me podréis negar que es aún más increíble si pensamos que uno de los principales desarrolladores de esta idea es una persona ciega.

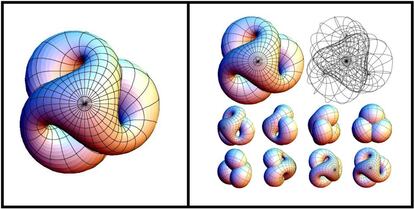
Aparte de esto, Morin fue el primero en dar una parametrización explícita de la conocida como superficie de Boy, descubierta por Werner Boy en 1901. Como detalle, comentar que esta superficie es una inmersión del plano proyectivo real en el espacio tridimensional, y genera imágenes tan maravillosas como ésta:

Lo que hizo Morin fue dar una forma explícita de describir esta superficie.

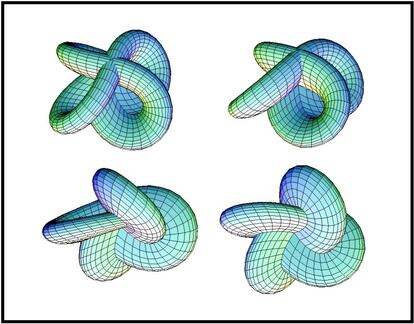
También tiene una superficie con su nombre, la superficie de Morin, que es algo así como la posición intermedia de la eversión de la esfera que él desarrolló, y que es algo así:

Otro ejemplo interesante de matemático ciego (y, curiosamente, también relacionado con la topología) es Louis Antoine. Suyo es un contraejemplo que nos dice que no hay un resultado análogo al teorema de la curva de Jordan en tres dimensiones. Tenéis más información sobre este contraejemplo, denominado collar de Antoine, en este artículo que escribí hace unos años.

¿Cómo pudo Morin llegar a este nivel en matemáticas siendo ciego? Pues, evidentemente, con mucha constancia y mucho tesón. Pero si nos ceñimos a los objetos geométricos y queremos profundizar un poco más, parece ser que Morin ha desarrollado una manera de relacionar el exterior y el interior de un objeto de forma táctil que le permite tener una gran compresión del mismo. Traduzco a continuación un párrafo de este gran artículo sobre Morin y otros matemáticos ciegos:

Algo complicado sobre visualización de objetos geométricos es que uno tiende a ver solamente el exterior de los objetos y no el interior, que podría ser muy complicado. Pensado cuidadosamente en las dos cosas a la vez, Morin ha desarrollado la habilidad de pasar del exterior al interior, o de una “habitación” a otra. Este tipo de imaginación espacial parece depender menos de las experiencias visuales que de las táctiles.

Al parecer, esta capacidad de Morin le permite recordar durante años la forma de un objeto simplemente con manipularlo durante un par de horas. Sencillamente impresionante.

El caso de Bernard Morin, del cual podéis ver algunas fotos en esta web de John Sullivan, es magnífico, maravilloso y cualquier otro adjetivo de sorpresa o admiración que se nos pueda ocurrir. Pero, como hemos visto con Louis Antoine, no es el único en matemáticas. Seguro que vosotros conocéis más casos (aparte de los que mencionan en el enlace que os dejé antes), tanto en matemáticas como en otros campos. Sería interesante que nos hablarais de ellos en los comentarios.