El problema de la mochila
Llenar una mochila de forma óptima puede ser un problema menos sencillo de lo que parece

Con la inflación disparada, es posible que una de las mejores opciones vacacionales, para algunas/os de mis amables lectoras/es, sea la de lanzarse a la aventura con una mochila al hombro, con lo que se les plantearía un problema de optimización de recursos, ya que se trataría de llevar un máximo de cosas útiles con un mínimo de peso. Una cuestión en apariencia sencilla, pero que entraña la suficiente complejidad potencial como para dar nombre a un importante capítulo de la optimización combinatoria, conocido precisamente como “problema de la mochila”, a menudo designado con las iniciales KP (del inglés Knapsack Problem).
Imagina que tienes a tu disposición un abundante suministro de paquetes de los siguientes pesos y precios:
12 kilos, 4 euros
4 kilos, 10 euros
2 kilos, 2 euros
1 kilo, 2 euros
1 kilo, 1 euro
¿Cómo llenarías tu mochila, en la que no puedes cargar más de 15 kilos, para maximizar el valor de su contenido?
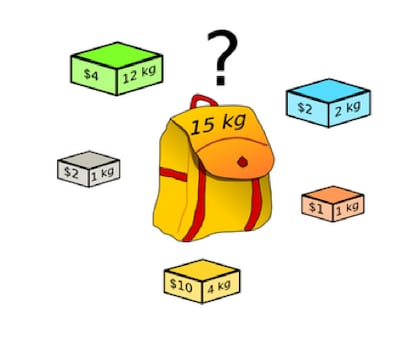
Y el metaproblema de rigor: ¿por qué he puesto este ejemplo tan aparentemente banal? Pues porque, navegando por la red en busca de datos curiosos y anécdotas sobre el tema, continuamente aparece esta mochila de 15 kilos con sus paquetes o cajas de los cinco tipos enumerados (generalmente con los precios en dólares). ¿Por qué será?
El problema de la mochila está directamente relacionado con el problema de la suma de subconjuntos, de gran importancia en criptografía y en teoría de la complejidad:
Dado un conjunto de números enteros, determinar si existe algún subconjunto no vacío tal que la suma de sus elementos sea cero.
Para un conjunto con pocos elementos, la cuestión es trivial. Por ejemplo, en el caso {2, 3, 4, 7, 10} la respuesta es obviamente “no”, pues todos los números son positivos, y en el caso {-3, -2, 2, 5, 6} la respuesta es “sí”, porque en el subconjunto {-3, -2, 5}, 5-3-2 = 0. Pero para conjuntos grandes la cosa se complica extraordinariamente, dada la dificultad computacional de examinar uno por uno todos los casos posibles, lo que lleva a aplicar distintos tipos de algoritmos tendentes a simplificar los cálculos a la vez que se minimiza el margen de error.
El problema del cambio de monedas
Retomando el tema monetario, al que dedicamos varias entregas hace unas semanas, es evidente el paralelismo entre el problema de la mochila y el denominado “problema del cambio de monedas”, que consiste en hallar el menor número de monedas (de diversos valores previamente especificados) que sumen una determinada cantidad.
Una forma de abordar el problema del cambio es aplicar un “algoritmo voraz” (ver Voracidad y optimización), que consiste en ir restando del valor buscado, una tras otra, las monedas de mayor valor posible. Por ejemplo, si he de devolver 80 céntimos, primero doy una moneda de 50 céntimos (que es la mayor que puedo restar de 80), luego una de 20 (que es la mayor que puedo restar de 30) y luego una de 10 (que es la mayor que puedo restar de 10). En este caso, la solución es óptima, pues no puedo dar 80 céntimos con menos de tres monedas (80 = 50 + 20 + 10). ¿Será siempre así, o habrá casos en los que el algoritmo voraz no reducirá al mínimo el número de monedas?
Y una cuestión práctica directamente relacionada con lo anterior: ¿está bien diseñado nuestro sistema monetario (el del euro) o es mejorable? Dicho de otro modo: ¿convendría añadir o eliminar algún valor para facilitar o simplificar las transacciones monetarias? Siempre he pensado que la moneda de 2 euros no tiene mucho sentido, pero…
Puedes seguir a MATERIA en Facebook, Twitter e Instagram, o apuntarte aquí para recibir nuestra newsletter semanal.
Tu suscripción se está usando en otro dispositivo
¿Quieres añadir otro usuario a tu suscripción?
Si continúas leyendo en este dispositivo, no se podrá leer en el otro.
FlechaTu suscripción se está usando en otro dispositivo y solo puedes acceder a EL PAÍS desde un dispositivo a la vez.
Si quieres compartir tu cuenta, cambia tu suscripción a la modalidad Premium, así podrás añadir otro usuario. Cada uno accederá con su propia cuenta de email, lo que os permitirá personalizar vuestra experiencia en EL PAÍS.
En el caso de no saber quién está usando tu cuenta, te recomendamos cambiar tu contraseña aquí.
Si decides continuar compartiendo tu cuenta, este mensaje se mostrará en tu dispositivo y en el de la otra persona que está usando tu cuenta de forma indefinida, afectando a tu experiencia de lectura. Puedes consultar aquí los términos y condiciones de la suscripción digital.
Sobre la firma







































































